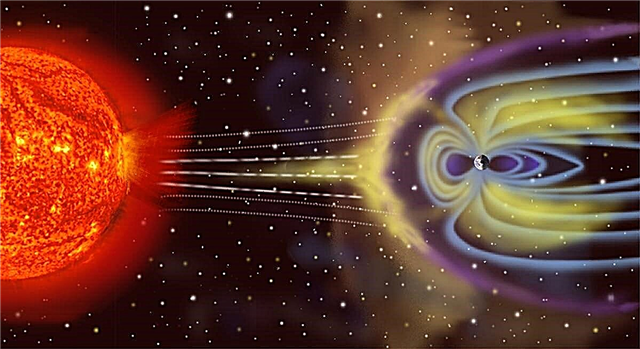
La relativité générale est une théorie complexe, mais imaginer la chute d'objets peut aider à tracer ses contours. (Ici, les satellites GPS sont représentés autour de la Terre - le GPS dépend de la relativité pour donner des positions précises.)
(Image: © NASA)
Paul Sutter est astrophysicien à Université d'État de l'Ohio et le scientifique en chef de Centre scientifique COSI. Sutter est également l'hôte de "Demandez à un astronaute" et "Radio spatiale"et prospects AstroTours autour du monde. Sutter a contribué à cet article Les voix d'experts de Space.com: Op-Ed & Insights.
La relativité générale est l'un des plus grands exploits de la compréhension humaine, d'autant plus impressionnant qu'elle est née de l'imagination fertile et de la brillance mathématique obstinée d'un seul esprit. La théorie elle-même est le dernier et le plus persistant des modèles "classiques" (c'est-à-dire non quantiques) de la nature, et notre incapacité à trouver quelque chose de plus sophistiqué au cours des cent dernières années nous rappelle constamment à quel point Dang smart Albert Einstein l'était.
Un autre témoignage du génie d'Einstein vient des spaghettis enchevêtrés d'équations complexes et interconnectées qui constituent la théorie complète. Einstein a fait une belle machine, mais il ne nous a pas exactement laissé de manuel d'utilisation. Nous pouvons retracer son chemin au cours des sept années de torture auto-infligée qui ont conduit à la forme finale de la théorie, mais cette voie de développement a été guidée par tellement d'intuition intestinale d'Einstein qu'il est difficile pour nous, simples mortels, de faire les mêmes sauts aveugles de le génie qu'il a fait.
Juste pour enfoncer le clou, la relativité générale est si complexe que lorsque quelqu'un découvre une solution aux équations, il obtient le nom de la solution et devient semi-légendaire à part entière. Il y a une raison pour laquelle Karl Schwarzschild - le gars qui a compris la géométrie des trous noirs - est un nom familier (ou du moins, un nom de département de physique). [Théorie de la relativité générale d'Einstein: une explication simplifiée]
La géométrie est le destin
Le noyau absolu de la relativité générale, et un nom alternatif parfaitement acceptable, est la géométrodynamique. Allez-y, dites-le à haute voix - c'est amusant. La manière dont la relativité générale modélise la gravité passe par les machinations dynamiques de l'espace-temps lui-même. Selon la théorie, la présence de matière et d'énergie modifie la géométrie fondamentale de l'espace-temps entourant ces substances, et cette géométrie modifiée influence le mouvement.
Cette relation découle du concept le plus important, fondamental, incontournable, qui sous-tend toute la théorie de la relativité générale: le principe d'équivalence (E.P.). Ce principe est l'hypothèse que la masse inertielle (combien de poussée il faut pour déplacer un objet) est la même propriété que la masse gravitationnelle (combien un objet répond à la gravité). Et c'est la clé qui déverrouille l'ensemble du shebang gravitationnel.
En utilisant cette équivalence, nous pouvons imaginer un scénario pour aider à visualiser le lien entre la géométrie et la gravité. Imaginez que vous êtes en orbite au-dessus de la Terre, en regardant sereinement les continents et les océans rouler sous votre point de vue.
Ensuite, vous ouvrez une boîte de déchets.
Alors que les débris flottent loin de vous, vous réfléchissez aux ramifications de ce que vous venez de faire. Bien sûr, vous avez maintenant créé un nuage de débris potentiellement dangereux qui présente un risque majeur pour les satellites et les futures missions. Mais après réflexion, votre esprit se calme. Vous faites une expérience scientifique et le principe d'équivalence garantit que tous ces morceaux de débris, quelle que soit leur forme ou leur masse, retraceront parfaitement les effets de la gravité de la Terre, sans avoir besoin d'autres calculs. C'est quelque chose d'unique à la force de gravité, grâce à l'E.P. [Pourquoi la relativité est vraie: les preuves de la théorie d'Einstein]
Plier les règles
Regardez ce qui arrive aux déchets que vous avez jetés dans l'espace. Certains, par pur hasard, peuvent commencer sur une ligne parfaitement horizontale. Mais lorsque les objets tombent sur la Terre, ils suivent des lignes droites se dirigeant vers le centre du globe. Si vous les observez de près, vous verrez que lorsqu'ils se dirigeront vers le bas, ils convergeront progressivement. S'ils pouvaient traverser la Terre solide, ils finiraient par entrer en collision au centre même.
D'autres débris pourraient commencer dans une ligne parfaitement verticale dirigée vers la Terre, régulièrement espacée les uns des autres. Eux aussi tomberaient. Mais le chanceux en tête de ligne tomberait légèrement plus vite, en raison de sa proximité légèrement plus proche de la Terre, le dernier en ligne étant légèrement en retard. Ainsi, alors que les débris poursuivaient leur descente, ils divergent lentement dans leur ligne verticale.
Dans certains cas, nous obtenons des sentiers convergents et rétrécissants. Dans d'autres cas, nous obtenons des trajectoires divergentes et étalées. Dans les deux cas, les chemins commencent comme parfaitement parallèles ou uniformes mais changent de caractère s. Ces trajectoires changeantes sont exactement ce que les mathématiciens utilisent pour décrire le langage de la «courbure», et c'est le langage de la géométrie.
Ding, ding, ding. Le voilà. Le principe d'équivalence vous dit que les chemins de la jonque qui tombe vous informent directement sur la nature de la gravité, et ces mêmes chemins révèlent une géométrie compliquée de l'espace-temps sous-jacent. En d'autres termes, cette gravité est la géométrie de l'espace-temps.
Géométrodynamique.
Étirer nos cerveaux
Le «temps» dans l'espace-temps est très important pour la théorie complète. Vous avez probablement vu la démo ou le graphique du musée des sciences accompagnant un article sur la relativité générale montrant à quoi ressemble une feuille de caoutchouc étirée. Une balle lourde, représentant une planète ou une étoile ou un trou noir ou autre, est placée au centre, tirant le tissu vers le bas. Faire rouler d'autres boules sur la feuille révèle "l'influence" de la gravité: ils essaient de suivre des lignes droites, mais leurs trajectoires sont déviées par la courbure sous-jacente.
Cette démo est parfaitement bien comme une première introduction à la maternelle, mais nous avons bien dépassé la maternelle maintenant. Il n'y a pas de "bas" dans l'espace-temps réel, et la courbe se produit en quatre dimensions, pas deux. C'est un peu plus difficile à visualiser, c'est pourquoi nous nous retirons généralement vers la démo plus simple.
Il est vrai qu'un objet massif déforme l'espace statique à proximité, mais ce n'est que la moitié de l'image. La masse affecte également la dimension du temps, et elle le fait en modifiant les trajectoires possibles dont un objet qui passe est capable.
Chaque objet a ce qu'on appelle un cône de lumière, ou un ensemble de destinations possibles que l'objet pourrait atteindre en se déplaçant plus lentement que la vitesse de la lumière. Imaginez-vous chevaucher avec un grain de poussière qui court au soleil. Il a une gamme de possibilités futures, donnée par son cône de lumière. Mais à mesure que la poussière s'approche du soleil, la gravité de cette boule de feu géante incline le cône de lumière de la poussière vers le soleil lui-même. La poussière a désormais un nouvel avenir plus spécifique qui lui est assigné: certaines destinations sont interdites (elles sont en dehors du nouveau cône lumineux), tandis que d'autres se sont ouvertes.
Cela peut sembler diviser les cheveux, mais la flexion statique de l'espace et la modification des cônes de lumière apparaissent dans les mathématiques de la relativité générale à des endroits séparés, et ce n'est qu'en combinant les deux effets que nous obtenons les prédictions complètes (et précises!) Des théorie. L'espace et le temps doivent être considérés ensemble; vous ne pouvez pas ignorer one.u
En d'autres termes, la gravité est la géométrie de l'espace-temps. Géométrodynamique.
Pour en savoir plus, écoutez l'épisode "" Sérieusement, qu'est-ce que la gravité? (Part 3) "sur le podcast" Ask A Spaceman ", disponible sur iTunes et sur le Web à http://www.askaspaceman.com. Merci à Andrew P., Joyce S., @ Luft08, Ben W., Ter B., Colin E, Christopher F., Maria A., Brett K., bryguytheflyguy, @MarkRiepe, Kenneth L., Allison K., Phil B. et @shrenic_shah pour les questions qui ont mené à cette pièce! Posez votre propre question sur Twitter en utilisant #AskASpaceman ou en suivant Paul @ PaulMattSutter et facebook.com/PaulMattSutter. Suivez-nous @Spacedotcom, Facebook et Google+. Article original sur Space.com.